Heat exchanger take heat from one fluid and pass it to a second. The fire-tube array of a steam engine is a heat exchanger, taking heat from the hot combustion gases of the firebox and transmitting it to the water in the boiler. The network of finned tubes in an air conditioner is a heat exchanger, taking heat from the air of the room and dumping it into the working fluid of the conditioner. The radiator in a car performs a similar function. The key element in heat exchanger is the tube wall or membrane which separates the two fluids. It is required to transmit heat and there is frequently a large pressure difference across it.
The Model
First, a little background on heat flow. Heat transfer from one fluid, through a membrane to a second fluid, involves convective transfer from fluid 1 into the tube wall, conduction through the wall, and convection again to transfer it into fluid 2. The heat flux q into the tube wall by convection (in units of W/m2) is described by the heat transfer equation:
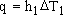 (1)
(1)
in which h1 is the heat transfer coefficient and DT1 is the temperature drop across the surface from fluid 1 into the wall. Conduction is described by the conduction (or Fourier) equation
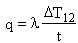 (2)
(2)
where l is the thermal conductivity of the wall (thickness t) and D T12 is the temperature difference across it.
It is helpful to think of the thermal resistance at surface 1 as 1/h1; that of surface 2 is 1/h2; and that of the wall itself is t/l. Then continuity of heat flux requires that the total resistance 1/U is
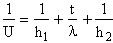 (3)
(3)
where U is called the 'total heat transfer coefficient '. The heat flux from fluid 1 to fluid 2 is then given by
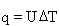 (4)
(4)
where DT is the difference in temperature between the two working fluids. When one of the fluids is a gas, as in an air conditioner, heat transfer at the tube surface contributes most of the resistance; then fins are used to increase the surface area across which heat can be transferred. But when both working fluids are liquid, convective heat transfer is rapid and conduction through the wall dominates the thermal resistance. In this case simple tube elements are used, with their wall as thin as possible to maximise l/t. We will consider the second case: conduction limited heat transfer. Then 1/h1 and 1/h2 are negligible when compared with t/l, and the heat transfer equation becomes
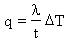 (5)
(5)
Consider, now, a heat exchanger with many tubes, each of radius r and wall thickness t with a pressure difference Dp between the inside and outside. Our aim is to select a material to maximise the total heat flow, while safely carrying the pressure difference Dp. The total heat flow is
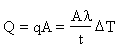 (6)
(6)
where A is the total surface area of tubing.
This is the objective function. The constraint is that the wall thickness must be sufficient to support the pressure difference Dp. This requires that the stress in the wall remain below the elastic limit (yield strength) sel (times a safety factor, which need not be included in this analysis):
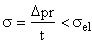 (7)
(7)
Eliminating t between the last two equations gives
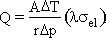 (8)
(8)
The heat flow per unit area of tube wall, Q/A, is maximised by maximising the performance index:
 (9)
(9)
Four further considerations enter the selection. It is essential to choose a material that withstands corrosion in the working fluids, which we take here to be water containing chloride ions (sea water). Cost will naturally be of concern. The maximum service temperature must be adequate and the material should be available as drawn tube.
What are the best materials for making heat exchanger? Or, more specifically, what are the best materials for a conduction-limited exchanger, with substantial pressure difference between the two fluids? 